● 자료의 대표값
자료의 특성을 몇 가지 대표값으로 표현하고자 할 때, 크게는 자료의 중심위치에 관한 측도와 자료의 산포도에 관한 측도 등의 두 가지가 가장 일반적이라고 할 수 있습니다. 그런데 자료는 대부분 모집단(population)에서 얻은 표본(sample)이기 때문에 그 측도들도 모집단과 표본에서의 정의가 조금씩 다를 수 있습니다.

● 모수와 표본통계량
모집단은 우리가 관심을 갖는 대상전체를 의미합니다. 우리는 이러한 집단의 특정한 값에 관심을 갖는데 이를 모수(parameter)라 칭합니다. 그리고 이러한 모수의 값을 짐작하기 위하여 우리가 얻은 표본들을 적당한 함수형태로 바꾸는데, 이를 표본 통계량(sample statistic)이라 부릅니다.

● 모수와 표본통계량의 구체적인 예시
예를 들어 우리나라 PC방의 월평균 게임사용시간을 조사하고자 무작위로 1,500개의 PC방을 뽑아 조사하였다면 위 용어들의 구체적 내용은 다음과 같습니다.
- 모집단 : 우리나라 전체 PC방
- 모수 : 월평균 게임사용시간
- 표본 : 무작위로 뽑힌 PC방들의 월 게임사용시간
- 표본통계량 : 표본들의 산술평균 또는 중앙값 등

(1) 중심위치에 관한 측도

가. 평균
평균(mean)은 가장 많이 사용되는 자료 중심의 관한 측도로서, 모든 자료의 합을
자료의 개수로 나눈 것입니다.








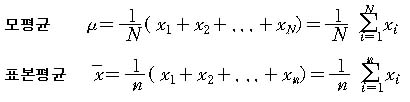
나. 중앙값
자료를 크기 순서대로 나열했을 때 가운데에 위치하는 값을 중앙값(median)이라고 합니다. 자료의 수가 짝수일 때는 중앙에 위치하는 수가 2개이므로 이들의 평균을 사용합니다.
가령 아래와 같은 자료가 있다고 가정합니다.
1.2 1.4 1.6 1.9 21

이 자료의 평균은 5.42로 급격히 변하지만 중앙값은 1.6으로 변화가 없습니다. 평균은 저울의 무게중심과 같아서 자료의 이상값(outlier : 데이터의 정상적인 범주를 벗어나는 값, 입력오류나 이상개체의 출현 등으로 발생)에 크게 영향을 받지만 중앙값은 영향을 거의 받지 않습니다.

그러나 중앙값은 가운데 값 외에는 순서 정보만 이용하고 구체적인 값에 대한 정보를 무시하게 되어, 모든 자료를 다 이용하는 평균에 비해 정보의 손실이 많습니다. 반대로 평균은 정보의 손실이 적은 반면 이상값에 매우 민감한 약점이 있습니다.

다. 최빈값
최빈값(mode)은 자료 중 빈도수가 가장 높은 값(또는 계급, 항목 등)을 뜻합니다. 예를 들어 온라인 RPG게임의 총사용시간에 대한 자료를 얻었을 때, 총사용시간의 분포형태는 좌우대칭이 아니고 한쪽으로 기울어진 형태이므로, 평균은 자료의 중심위치에 대한 좋은 측도가 되지 못합니다.(흔히 총사용시간은 인기가 많은 RPG 게임쪽으로 기웁니다.) 이때는 평균보다는 중앙값, 그리고 중앙값과 더불어 최빈값 등을 출력하여 대부분의 총사용시간이 더이데 집중되어 있는가를 표현해 주는 것이 바람직합니다.